Insertion sort

Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages:

• Simple implementation
• Efficient for (quite) small data sets
• Adaptive (i.e., efficient) for data sets that are already substantially sorted: the time complexity is O(n + d), where d is the number ofinversions
• More efficient in practice than most other simple quadratic (i.e., O(n²)) algorithms such as selection sort or bubble sort; the best case (nearly sorted input) is O(n)
• Stable; i.e., does not change the relative order of elements with equal keys
• In-place; i.e., only requires a constant amount O(1) of additional memory space
• Online; i.e., can sort a list as it receives it

When humans manually sort something (for example, a deck of playing cards), most use a method that is similar to insertion sort.^[1]

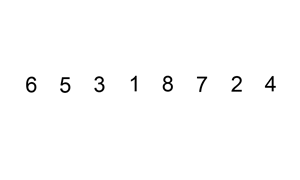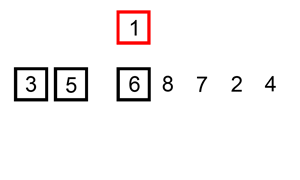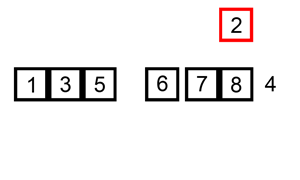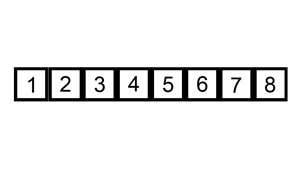
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

package com.java2novice.algos;   public class MyInsertionSort {       public static void main(String[] args) {                   int[] input = { 4, 2, 9, 6, 23, 12, 34, 0, 1 };         insertionSort(input);     }           private static void printNumbers(int[] input) {                   for (int i = 0; i < input.length; i++) {             System.out.print(input[i] + ", ");         }         System.out.println("\n");     }       public static void insertionSort(int array[]) {         int n = array.length;         for (int j = 1; j < n; j++) {             int key = array[j];             int i = j-1;             while ( (i > -1) && ( array [i] > key ) ) {                 array [i+1] = array [i];                 i--;             }             array[i+1] = key;             printNumbers(array);         }     } }

Pseudocode of the complete algorithm follows, where the arrays are zero-based:

// The values in A[i] are checked in-order, starting at the second one
for i ← 1 to i ← length(A)
  {
    // at the start of the iteration, A[0..i-1] are in sorted order
    // this iteration will insert A[i] into that sorted order
    // save A[i], the value that will be inserted into the array on this iteration
    valueToInsert ← A[i]
    // now mark position i as the hole; A[i]=A[holePos] is now empty
    holePos ← i
    // keep moving the hole down until the valueToInsert is larger than 
    // what's just below the hole or the hole has reached the beginning of the array
    while holePos > 0 and valueToInsert < A[holePos - 1]
      { //value to insert doesn't belong where the hole currently is, so shift 
        A[holePos] ← A[holePos - 1] //shift the larger value up
        holePos ← holePos - 1       //move the hole position down
      }
    // hole is in the right position, so put valueToInsert into the hole
    A[holePos] ← valueToInsert
    // A[0..i] are now in sorted order
  }